ایجاد نسبت طلایی عبارت است از تقسیم پاره خط به دو قسمت به طوری که نسبت طول قطعه بزرگ تر به طول تمام پاره خط، مساوی با طول قطعه کوچک تر به قطعه بزرگ تر باشد. این نسبت در قدیم به تقسیم خط به نسبت ذات وسطین و طرفین (یا تقسیم توافقی) معروف بوده است که معادل آن به صورت اعشاری در حدود 1?618 خواهد بود که این عدد همان عدد فی می باشد و یکی از خواص آن این است که اگر یک واحد از آن کسر کنیم مقدار آن برابر عکس خودش می شود.
نتایج تحقیقات فراوان علمی و روان شناسی اعلام می کند که زیباترین سطوح و اشکال از نظر انسان ها، آنهایی هستند که در ابعاد آنها نسبت طلایی به کار رفته باشد.

تعبیر هندسی دیگر اینگونه‌است: پاره خط AB و نقطه? M روی آن مفروضند به گونه‌ای که نسبت a به b برابر است با نسبت a+b به a. این نسبت برابر φ است. یعنی:

 پیشینه توجه به عدد طلایی نه به زمان فیبوناچی بلکه به زمانهای بسیار دورتر می‌رسد.اقلیدس در جلد ششم از سیزده جلد کتاب مشهور خود که در آنها هندسه اقلیدسی را بنا نهاد، این نسبت را مطرح کرده‌است. لوکا پاچیولی (The Divine Proportion) تالیف کرد. وی در آن نقاشی‌هایی از لئوناردو داوینچی آورده‌است که پنج جسم افلاطونی را نمایش می‌دهند و در آنها نیز به این نسبت اشاره شده‌است. در سال 1509 میلادی کتابی با عنوان نسبت الهی

مصریان، سالها قبل از میلاد از این نسبت آگاه بوده‌اند و آن را در ساخت اهرام مصر رعایت کرده‌اند. بسیاری از الگوهای طبیعی در بدن انسان این نسبت را دارا هستند. نسبت طول ضلع پنج پر منتظم به طول ضلع پنج ضلعی منتظم برابر همین عدد است. روانشناسان هم بر این باورند زیباترین مستطیل به دید انسان، مستطیلی است که نسبت طول به عرض آن برابر عدد طلایی باشد.

.

نسبت طلایی در ایران:

برج و میدان آزادی :طول بنا 63 و عرض ان 42 است که 5/1=42 : 63 و به عدد طلایی نزدیک می‌باشدسبک معماری آن نیزطاق بزرگی است که تلفیقی از سبک هخامنشی و ساسانی و اسلامی است که منحنی آن با الهام از طاق کسری معماری ایران باستان را تداعی می نماید.

قلعه دالاهو , کرمانشاه :خطی از استحکامات به طول دو و نیم کیلومتر و عرض چهار متر با قلوه و لاشه سنگ به همراه ملاط دیوار گچ را می سازد. سرتاسر نمای خارجی این دیوار با مجموعه‌ای از برج های نیم دایره‌ای شکل تقویت شده است.می دانیم6/1=5/2 : 4 که همان عدد طلایی است.

بیستون از دوره هخامنشی , کرمانشاه:به طول 5 کیلومتر و عرض 3 کیلومتراست.اعداد5و3هردوجزودنباله فیبوناتچی هستندو6/1=5:3 و ابعاد برجسته کاری 18 در 10 پاست که قامت “داریوش”5 پا و 8 اینچ (170 سانتیمتر)بلندی داردکه هر دو اعداد فیبوناتچی هستند پل ورسک در مازندران:این پل بر روی رودخانه ورسک در مجاورت سواد کوه بنا شد.بلندی این پل 110 متر است وطول قوس آن 66 متر می‌باشد(6/1 = 66 : 110 ).

مقبره ابن سینا:آرامگاه دروسط تالاری مربع شکل قرارگرفته که پله مدور(مارپیچ فیبوناتچی) و پایه‌های دوازده گانه برج را احاطه کرده اند .سطح حیاط باسه پله سراسری به ایوان متصل است.ایوان با دری به ارتفاع 2/3 متر و عرض 9/1 متر به سرسرای آرامگاه متصل است (6/1=9/1 : 2/3 )در دو طرف سرسرا دو تالار قرار دارد یکی در جنوب که تالار سخنرانی و اجتماعات است.و یکی در شمال که کتابخانه آرامگاه است.طول تالار کتابخانه 45/9 متر وعرض آن 75/5 متر است(6/1=75/5 : 45/9 )

ارگ بم :این بنا 300 متر طول و 200 متر عرض داشته و از 2 قسمت تشکیل شده است. این دژ 5 شیوه ساختاری از خشت خام دارد . (3 و 2 و 5 اعداد دنباله فیبوناتچی هستند)

محاسبه:

برای بدست آوردن نسبت طلائی از تعریف هندسی آن استفاده می‌کنیم:

از این معادله که تعریف عدد است، که از معادله سمت راست می‌توان نتیجه گرفت: ، پس خواهیم داشت:

با حذف b از طرفین به دست می‌آید:

پس از ساده سازی این معادله، معادله درجه دومی بر حسب به دست می‌آید:

و پاسخ مثبت آن:

که همان نسبت طلائی است.

این نسبت از قدیم در بین هنرمندان و معماران شناخته شده و در آثار خود از آن استفاده می کرده اند؛ نظیر ساختمان معبد پارتنون که در آن این نسبت به کار رفته است.

.

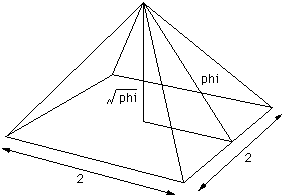
در اهرام مصر نیز این نسبت به دقت رعیات شده است. مثلث قائم الزاویه ای که با نسبت های این هرم شکل گرفته شده باشد به مثلث قائم مصری یا Egyptian Triangle معروف هست و جالب اینجاست که بدانید نسبت وتر به ضلع هم کف هرم معادل با نسبت طلایی یعنی دقیقا 1?61804 می باشد. این نسبت با عدد طلایی تنها در رقم پنجم اعشار اختلاف دارد یعنی چیزی حدود یک صد هزارم!

.

مدارک به دست آمده از دو هزارسال قبل از میلاد در یکی از اهرام مصر نیز که در یکی از اطاق ها تصویری به دست آمده، حاکی از مطالعه این نسبت روی اجزای بدن انسان است که مطالعه آن توسط لوکوربوزیه معمار فرانسوی روی بدن انسان، جدول معروفی را به دست می دهد که با استفاده از قابلیت تقسیم طبیعی در بدن انسان، علم نسبت ها را در ساختمان وارد کرده است. بررسی های لوکوربوزیه بعد از وی توسط دیگر دانشمندان مورد مطالعه و پیگیری است.

لئوناردو داوینچی در ترسیم نقاشی معروف خود از بدن انسان از نسبت طلایی بهره گرفته است. به عنوان مثال نقاطی از بدن که دارای نسبت طلایی هستند:
نسبت قد انسان به فاصله ناف تا پاشنه پا.
نسبت فاصله نوک انگشتان تا آرنج به فاصله مچ تا آرنج.
نسبت فاصله شانه تا بالای سر به اندازه سر.
نسبت فاصله ناف تا بالای سر به فاصله شانه تا بالای سر.
نسبت فاصله ناف تا زانو به فاصله زانو تا پاشنه پا.

انتخاب ده ضلعی منتظم از طرف هنرمندان ایرانی و استفاده آن در کارهای معماری (پوشش گنبدها با کاربندی ده) و کارهای هنری (گره سازی ها که پایه آنها روی ده ضلعی منتظم قرار دارد) توجه و دقت آنها و بالاخره دید آنها را در انتخاب و به دست آوردن بهترین تناسبات در خطوط و سطوح را می رساند. چرا که در ده ضلعی منتظم نسبت شعاع به طول ضلع، همان نسبت طلائی است که در تمام کاربندی پوشش های گنبدی در معماری اصیل ایرانی – اسلامی از آن استفاده شده است.

همچنین مثلث متساوی الساقینی که ابوالوفاء بوزجانی در کشیدن پنج ضلعی از آن استفاده کرده و آن را مثلث پنج ضلعی نامیده است، مثلثی است که بین ساق و قاعده آن این نسبت طلایی وجود دارد.

در مطالعه در طبیعت نیز این تناسب زیاد دیده می شود نظیر فاصله برگ های روی ساقه و ساقه روی شاخه و شاخه روی تنه در بعضی گیاهان که بین هر دو زوج، سومی تقریبا در جای طلایی قرار گرفته است.

پوسته مارپیچی یک حلزون نمونه ای ساده و درعین حال زیبا از نسبت طلائی است.

.

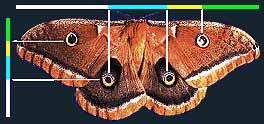
نسبت طلایی در فواصل خال های پروانه

.

نسبت طلائی در فواصل افقی قطعات ویولون

رعایت نسبت طلایی در طول و عرض iPod نسبت به محصولات مشابه

برش اهرام و نسبت طلایی

مثلث قائم الزاویه ای که با نسبت های این هرم شکل گرفته شده باشد به مثلث قائم مصری یا Egyptian Triangle معروف هست و جالب اینجاست که بدانید نسبت وتر به ضلع هم کف هرم معادل با نسبت طلایی یعنی دقیقا” 1?61804 می باشد. این نسبت با عدد طلایی تنها در رقم پنجم اعشار اختلاف دارد یعنی چیزی حدود یک صد هزارم. باز توجه شما را به این نکته جلب می کنیم که اگر معادله فیثاغورث را برای این مثلث قائم الزاویه بنویسم به معادله ای مانند phi²=phi+b² خواهیم رسید که حاصل جواب آن همان عدد معروف طلایی خواهد بود. (معمولا” عدد طلایی را با phi نمایش می دهند)

طول وتر برای هرم واقعی حدود 356 متر و طول ضلع مربع قاعده حدودا” معادل 440 متر می باشد بنابر این نسبت 356 بر 220 (معادل نیم ضلع مربع) برابر با عدد 1?618 خواهد شد.

کپلر (Johannes Kepler 1571-1630) منجم معروف نیز علاقه بسیاری به نسبت طلایی داشت بگونه ای که در یکی از کتابهای خود اینگونه نوشت : “هندسه دارای دو گنج بسیار با اهمیت می باشد که یکی از آنها قضیه فیثاغورث و دومی رابطه تقسیم یک پاره خط با نسبت طلایی می باشد. اولین گنج را می توان به طلا و دومی را به جواهر تشبیه کرد”.

تحقیقاتی که کپلر راجع به مثلثی که اضلاع آن به نسبت اضلاع مثلث مصری باشد به حدی بود که امروزه این مثلث به مثلث کپلر نیز معروف می باشد.

منابع :

http://fa.wikipedia.org

http://www.senmerv.com

http://www.newdesign.ir

http://www.nimapedia.mihanblog.com